Welcome to the world of linear equations! This section introduces word problems, focusing on practical applications and problem-solving strategies. Worksheets are essential for mastering these skills, offering structured practice and real-world relevance.
1.1 Overview of Linear Equations

A linear equation is a mathematical expression of the first degree, where the highest power of the variable is 1. It can be written in the form of ( ax + b = 0 ), where ( a ) and ( b ) are constants, and ( x ) is the variable. Linear equations are fundamental in algebra and are used to model real-world problems involving direct proportions or constant rates of change. They can have one or more variables, but the degree of each variable remains 1. These equations are essential for solving word problems, as they simplify complex scenarios into manageable mathematical relationships. Understanding linear equations is a cornerstone of problem-solving, enabling students to analyze and interpret data effectively. Worksheets dedicated to linear equations word problems provide structured practice, helping learners grasp these concepts and apply them to various situations. Regular practice enhances problem-solving skills and builds a strong foundation in mathematics.
1.2 Importance of Word Problems in Learning

Word problems are a vital component of mathematics education, as they bridge the gap between abstract equations and real-world scenarios. They require students to interpret and translate textual information into mathematical expressions, enhancing their critical thinking and problem-solving abilities. By incorporating linear equations into word problems, learners develop a deeper understanding of how these equations apply to practical situations, such as budgeting, distance calculations, or resource allocation. Word problems also foster analytical skills, as students must identify relevant information, set up equations, and solve them accurately. Worksheets dedicated to linear equations word problems provide a structured way to practice these skills, ensuring mastery and confidence. Regular exposure to word problems prepares students for more complex mathematical challenges and equips them with the tools to tackle real-life problems effectively. This approach makes learning engaging and meaningful, connecting theory to application.

1.3 Benefits of Using Worksheets
Worksheets are an invaluable resource for mastering linear equations word problems. They provide structured, organized practice, helping students build a strong foundation in problem-solving. By offering a variety of exercises, worksheets enable learners to explore different scenarios and applications of linear equations. Regular practice with worksheets enhances critical thinking and analytical skills, as students learn to translate real-world situations into mathematical expressions. Worksheets also cater to different learning paces, allowing students to work independently and review concepts as needed. Additionally, they often include answer keys, enabling self-assessment and immediate feedback. This personalized approach fosters confidence and ensures a deeper understanding of the material. Worksheets are particularly useful for reinforcing classroom lessons and preparing for assessments. Their clarity and focus make them an essential tool for students aiming to excel in linear equations word problems.

Understanding Linear Equations
Linear equations represent relationships between variables in a straightforward form, often used to model real-world problems. They are foundational in algebra, enabling the solution of various practical and mathematical scenarios effectively.
2.1 Definition and Basic Concepts
A linear equation is an algebraic expression of degree one, where variables represent unknown values. It follows the form ax + b = 0, where a and b are constants, and x is the variable. The goal is to solve for x, isolating it on one side of the equation. Linear equations are fundamental in mathematics and real-life applications, such as budgeting, distance calculations, and mixtures. They can be graphed as straight lines on a coordinate plane, illustrating a constant rate of change. Understanding these basics is crucial for tackling word problems, which often require translating scenarios into mathematical expressions. Worksheets provide ample practice, ensuring mastery of these essential skills. Regular practice helps build confidence and fluency in solving linear equations efficiently.
2.2 Components of a Linear Equation
A linear equation consists of several key components: variables, coefficients, constants, and an equals sign (=). Variables are letters or symbols that represent unknown values, while coefficients are numbers that multiply these variables. Constants are numerical values without variables. The equals sign divides the equation into two expressions, ensuring balance. For example, in the equation 2x + 3 = 7, x is the variable, 2 is the coefficient, and 3 and 7 are constants. Linear equations can also include multiple variables, such as 3x + 4y = 11, where both x and y are variables. Understanding these components is vital for solving and interpreting word problems effectively. Worksheets often focus on identifying and working with these elements to build foundational skills in algebra.
2.3 Real-World Applications of Linear Equations
Linear equations are invaluable in real-world scenarios, providing straightforward solutions to everyday problems. They are widely used in budgeting, where equations help calculate expenses and income. For instance, determining how much to spend on groceries while staying within a budget can be modeled with a linear equation. Distance and speed problems, such as calculating travel time between two locations, also rely on linear equations. Additionally, resource allocation in businesses, like managing inventory or scheduling staff, often involves linear equations to optimize efficiency. Even in cooking, scaling recipes up or down requires proportional adjustments, which can be expressed as linear relationships. Worksheets focusing on these applications help learners connect mathematical concepts to practical, relatable situations, enhancing problem-solving skills and fostering a deeper understanding of algebraic principles in action.

Creating Effective Word Problems
Crafting clear, relevant word problems is essential for engaging students. Use real-world scenarios to make linear equations relatable and easier to understand, enhancing problem-solving skills effectively.

3.1 Steps to Formulate Word Problems
Formulating effective word problems involves several key steps. First, identify a real-world scenario that can be modeled using linear equations, such as budgeting, distance, or mixture problems. Next, define the variables and their relationships clearly. Use simple, concise language to describe the situation, ensuring the problem is easy to understand. Incorporate visual aids like diagrams or charts if necessary to enhance clarity. Finally, ensure the problem aligns with curriculum standards and includes a logical solution path. By following these steps, educators can create engaging and relevant word problems that help students apply linear equations to practical situations. This approach fosters critical thinking and problem-solving skills, making learning more interactive and meaningful.
3.2 Aligning Problems with Curriculum Standards
Aligning word problems with curriculum standards ensures that learning objectives are met effectively. Educators must first identify the specific skills and concepts outlined in the curriculum, such as solving linear equations or interpreting graphs. Next, they should design problems that directly target these skills, using real-world contexts that resonate with students. For example, problems involving budgeting or distance can illustrate practical applications of linear equations. Additionally, the difficulty level of the problems should match the grade level and proficiency of the students. Clear instructions and unambiguous language are crucial to avoid confusion. By structuring problems to align with curriculum standards, educators can ensure that worksheets are both educational and relevant, helping students build a strong foundation in linear equations and their applications.
3.3 Ensuring Clarity and Relevance

Ensuring clarity and relevance in word problems is crucial for effective learning. Clear language helps students focus on the mathematical concepts rather than getting confused by complex wording. Problems should be concise, avoiding unnecessary details that distract from the core equation. Relevance is equally important, as students are more engaged when problems relate to real-life scenarios or their interests. For example, problems involving budgeting, distance, or resource allocation are often more meaningful. Additionally, incorporating visual aids like diagrams or charts can enhance understanding. Feedback mechanisms, such as answer keys, allow students to verify their solutions and learn from mistakes. By balancing clarity and relevance, educators create worksheets that are both educational and engaging, helping students master linear equations through practical and relatable exercises.
Solving Linear Equations Word Problems
Mastering linear equations involves translating real-world scenarios into mathematical expressions. This section guides you through step-by-step solutions, emphasizing accuracy and practical applications to ensure a deep understanding of problem-solving techniques.
4.1 Step-by-Step Solution Process
Solving linear equation word problems involves a systematic approach. First, read the problem carefully and identify the unknown variable. Next, translate the words into a mathematical equation using constants, variables, and coefficients. Define the variable clearly and ensure the equation represents the problem accurately. Solve the equation by isolating the variable, checking each step for accuracy. Finally, verify the solution by substituting it back into the original problem to ensure it makes sense. Common steps include simplifying expressions, combining like terms, and performing inverse operations. Always check for reasonableness and consider if the answer aligns with real-world expectations. Practice with worksheets can help refine this process, making it second nature for students.
4.2 Checking Solutions for Accuracy
Verifying solutions is crucial to ensure correctness. After solving a linear equation, substitute the answer back into the original problem to confirm it makes sense. Check if the solution satisfies all conditions and constraints. Additionally, assess the reasonableness of the answer in the context of the problem. For example, if the problem involves time or distance, ensure the solution aligns with real-world expectations. Common mistakes include calculation errors or misinterpreting the problem. To avoid these, carefully review each step and consider alternative methods to confirm the solution. Using worksheets with answer keys can help students identify and correct errors. Regular practice enhances problem-solving skills and builds confidence in tackling word problems effectively. Always prioritize accuracy to develop a strong foundation in linear equations.
4.3 Common Mistakes and How to Avoid Them
When solving linear equation word problems, common mistakes include misinterpreting the problem, incorrect equation setup, and calculation errors. To avoid these, read the problem carefully and identify key information. Break down complex scenarios into simpler parts and define variables clearly. Double-check the equation setup before solving. Calculation errors can be minimized by working step-by-step and verifying each operation. Another mistake is ignoring negative solutions or not considering the context of the problem. Always ensure the solution makes sense in real-world terms. Regular practice with worksheets helps identify recurring errors. Use answer keys to review mistakes and understand where improvements are needed. By addressing these common pitfalls, students can enhance their problem-solving skills and achieve better results in linear equations word problems.

Designing a Worksheet in PDF Format
Creating a worksheet in PDF format involves selecting a clear layout, incorporating visuals, and adding answer keys. Ensure content is organized, visually appealing, and meets educational standards for effective learning.
5.1 Choosing the Right Layout
When designing a worksheet in PDF format, selecting the right layout is crucial for clarity and effectiveness. A clean, organized design ensures that content is easy to follow and visually appealing. Start by using a consistent grid or table format to align problems and solutions neatly. Proper spacing between questions and sections is essential to avoid clutter. Consider using headers or borders to separate different parts of the worksheet, such as problem statements, solution steps, and answer keys. Additionally, incorporate visual aids like diagrams or charts to enhance understanding, especially for complex problems. Ensure the font size and style are readable, with clear differentiation between instructions and content. Finally, include page numbers and a title to maintain professionalism and organization. A well-designed layout enhances the learning experience and makes the worksheet user-friendly for students and educators alike.
5.2 Incorporating Visual Aids
Incorporating visual aids into your linear equations word problems worksheet can significantly enhance learning and engagement. Graphs, charts, and diagrams help students visualize abstract concepts, such as slopes, intercepts, and relationships between variables. For example, include screenshots of graphing tools or hand-drawn illustrations to demonstrate how equations translate to real-world scenarios. Images of real-life applications, like distance-time graphs or budget plans, can make problems more relatable. Additionally, use tables or flowcharts to break down solution steps, making complex processes easier to follow. Ensure visuals are clear, labeled, and directly tied to the problems they illustrate. Avoid overcrowding the page; instead, balance text and visuals for a clean, professional look. By integrating relevant and well-designed visual aids, you create a resource that catersto different learning styles and deepens students’ understanding of linear equations. This approach makes the worksheet more interactive and effective for classroom or self-study use.
5.3 Adding Answer Keys and Feedback
Including answer keys and feedback in your linear equations word problems worksheet is essential for student learning and assessment. Provide clear, step-by-step solutions for each problem, ensuring students can track their progress and understand their mistakes. Place the answer key at the end of the worksheet or on a separate page for easy reference. Use boxes or highlighting to make answers stand out. Additionally, include brief explanations or tips to clarify common errors or tricky concepts. Feedback can also guide students on improving their problem-solving skills. For example, note areas where they might have made calculation mistakes or suggest alternative methods. This feature not only helps students verify their work but also reinforces their understanding of linear equations; A well-structured answer key with constructive feedback enhances the educational value of your worksheet, making it a comprehensive learning tool. Ensure the format is clean and easy to navigate for optimal usability.
Additional Resources and Tools
Explore online platforms for free linear equations worksheets, recommended software like Excel for creating custom problems, and interactive tools such as Khan Academy for enhanced practice and learning.
6.1 Where to Find Free Worksheets Online
Discover a wealth of free linear equations word problem worksheets online through platforms like Google Classroom, Teachers Pay Teachers, and MathWorks. These sites offer diverse resources tailored to various skill levels and educational needs.
Google Classroom provides accessible PDF formats, while Teachers Pay Teachers features community-shared content. MathWorks excels with STEM-focused materials. Additionally, Khan Academy and Pinterest host interactive tools and visual aids to enhance learning. When searching, look for worksheets aligned with curriculum standards and those offering answer keys for self-assessment. These platforms are invaluable for educators and students seeking quality practice materials without cost barriers.
6.2 Recommended Software for Creating Worksheets
Creating effective linear equations word problem worksheets is made easier with the right software. Microsoft Word and Google Docs are popular choices for their user-friendly interfaces and formatting options. For more specialized needs, tools like LaTeX offer precise mathematical typesetting, ideal for equations. Canva is excellent for designing visually appealing layouts, while Excel can help organize problems into structured tables. Additionally, educational software like SMART Notebook and Edmentum provide interactive features, enhancing worksheet creation for classroom use. These tools cater to different preferences and skill levels, ensuring educators can craft engaging and educational materials efficiently. By leveraging these resources, teachers can create worksheets that are both informative and visually appealing, supporting student learning and understanding of linear equations.
6.3 Interactive Tools for Practice
Interactive tools are invaluable for practicing linear equations word problems, offering dynamic and engaging learning experiences. Platforms like Khan Academy, GeoGebra, and Desmos provide interactive exercises and real-time feedback, helping students grasp concepts intuitively. Tools such as Mathway and Symbolab allow users to input problems and receive step-by-step solutions, fostering understanding and problem-solving skills. Additionally, apps like Photomath and Socratic utilize camera-based input to solve problems, making learning accessible on-the-go. These tools often include visual aids, such as graphs and animations, to simplify complex concepts. They also cater to different learning styles, ensuring that students can practice at their own pace. By leveraging these resources, learners can enhance their proficiency in solving linear equations word problems, building confidence and fluency in math. These tools are particularly useful for reinforcing classroom lessons and preparing for assessments. They make learning interactive, fun, and effective, ensuring long-term retention of skills.
Mastering linear equations through word problems enhances problem-solving skills and real-world application. Worksheets and interactive tools provide effective practice, reinforcing learning and building confidence in math abilities for all learners.
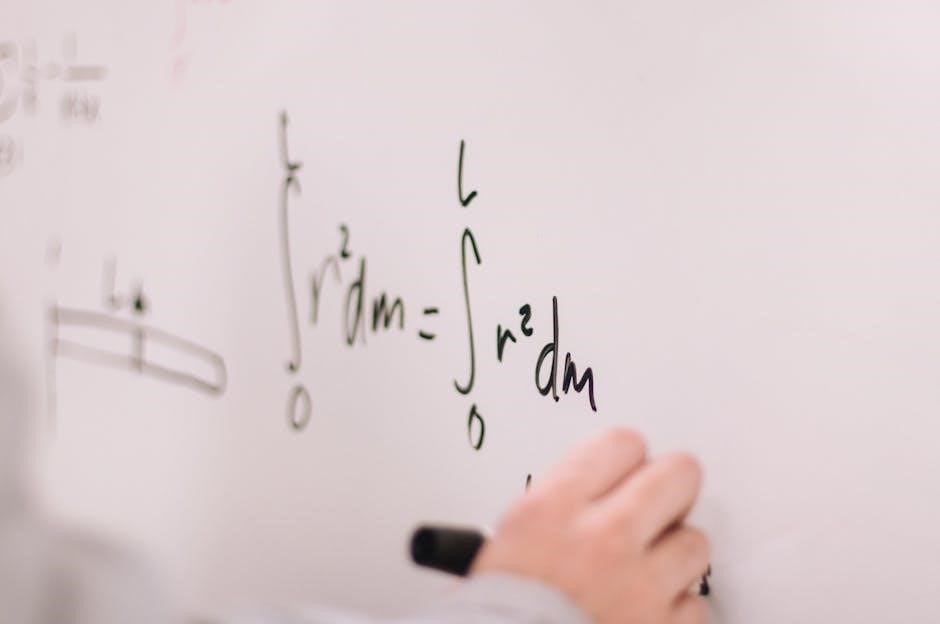
7.1 Summary of Key Points
7.2 Encouragement for Further Practice
Consistent practice is key to mastering linear equations word problems. Encourage learners to engage with worksheets regularly, as this builds confidence and problem-solving skills. Explore various resources, such as PDF worksheets, online tools, and educational apps, to make practice engaging. Set aside dedicated time for problem-solving and review past mistakes to improve understanding. Collaborating with peers or seeking feedback from educators can also enhance learning. Remember, perseverance and patience are essential for achieving proficiency. By staying committed and embracing challenges, learners will become adept at translating real-world scenarios into mathematical equations and solving them effectively. Keep practicing, and watch your skills grow!